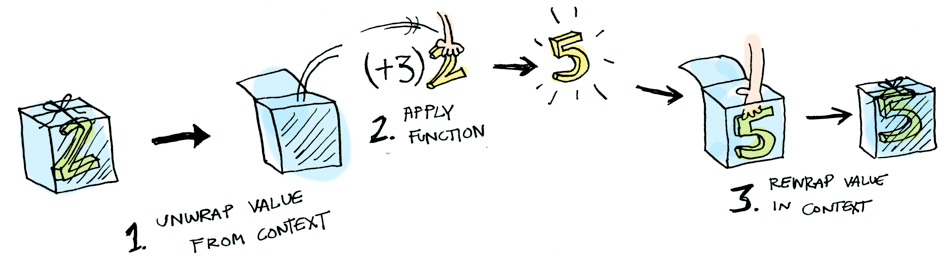현재 블로그를 함수형 프로그래밍 형태로 리팩토링 하기 전, 중요하다고 생각하는 개념들을 모두 훑은 다음 하기 위해

펑터와 관련된 포스트들을 가볍게 읽어보고 공부하며 적는 내용이다.

범주론과 관련하여 아주 엄밀하게 설명해주는 좋은 글 들이 있는데, 도저히 나의 머리로는 이해가 안가 최대한 포스팅 된 글들과 잼미니를 이용해서 교차검증하며 적은 글이다.

게시글에 들어가기 전 요약글

전체적인 맥락을 먼저 알고 보는 것이 더 나을 거 같아 요약글을 서문에 먼저 적는다.

1. 프로그래밍 세계에서 특정 값이 가지는 상황을 컨텍스트라 한다.
2. 이 때 함수 안에 들어갈 모든 데이터들이 하나의 컨텍스트를 가질 것이라 확신 할 수 없다. 예를 들어 유저 정보 가져오기 -> 가져온 유저 정보 대문자로 변경하기 라는 흐름 속에서 유저 정보가 항상 string이 아니라 null , undefined 등일 수도 있다. (유저 정보의 컨텍스트는 string | null | undefined)
3. 함수형 프로그래밍에서 값이 가질 수 있는 다양한 컨텍스트를 담을 자료구조가 필요하며, 그 자료구조가 Functor 이다.
4. Functor 는 값을 컨텍스트 안에 담을 뿐더러 다양한 연산을 통해 다른 Functor 들을 반환 가능하도록 하여 함수의 순차적 적용을 가능하게 한다.

펑터 (함자)란

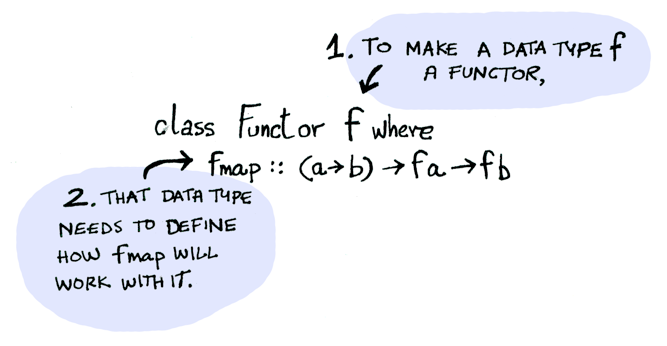펑터를 설명해주는 가장 좋은 예시

펑터란 어떤 데이터 타입 T 를 가졌으며 데이터 타입 T 를 다음과 같은 조건을 만족하는 함수들을 이용해 다른 데이터 타입을 가진 자료구조 (대부분 펑터)로 반환하는 함수를 가진 타입 클래스를 의미한다.

자바스크립트에서 가장 대표적이고 자주 사용했던 예시는 Array<T> 일 것이다.

Array<T> 는 어떤 데이터 타입 T 를 가지고 Array.prototype.map 메소드를 통해 (data : T)=> B 로 변환하는 순수함수를 인자로 주게 되면 Array<B> 를 반환하기 때문이다.

대표적인 함수형 프로그래밍 언어인 하스켈에선 이런 메소드를 fmap 이라 정의한다.

이 때 펑터는 항등 법칙과 합성 법칙을 만족해야 한다.

• 항등함수 id :: a -> a에 대해 fmap id :: f a -> f a도 항등함수다.
• 모든 함수 f :: b -> c와 g :: a -> b에 대해 fmap (f . g) ≡ fmap f . fmap g이다.

해당 표기법은 하스켈의 표기법으로 설명된 법칙이다. 표기법에 대해 정리하자면

1. :: 는 타입 선언을 의미한다. :: 를 기준으로 좌측은 어떤 함수의 이름, 입력값 -> 반환값 (범주론에선 어떤 입력값이 어떤 반환값으로 변경 되는 행위를 사상이라 이야기 한다.) 을 의미한다. 위 예시에서 id :: a -> a 는 id 라는 함수가 a 데이터를 받아 a 를 반환하는 것을 의미한다.

2. . 는 함수의 합성을 의미한다. f(a) , g(b) 라는 함수가 있을 때 f.g 는 f(g(a)) 를 의미한다.

3. 위 예시에 쓰인 f a 는 a 데이터 타입을 가진 Functor 를 의미한다.

4. ≡ 는 같음을 의미한다. 자바스크립트로 따지자면 === 와 같다.

자바스크립트 언어로 예시를 들어 이해해보자

항등 법칙

const Functor = <T>(value: T) => ({
  valueOf: value, 
  map: <U>(mapper: (value: T) => U) => Functor(mapper(value)), // fmap 역할
});

펑터 메소드 map 메소드가 또 다른 Functor 를 반환한다는 점을 상기하자

Functor<T>.map((data : T)=>U) 의 반환값은 Functor<U> 이다.

const functor = Functor(1);
const identity = (x: number) => x; // 위에서 예시로 들은 id 함수
const identityFunctor = functor.map(identity);
 
console.log(functor.valueOf === identityFunctor.valueOf); // true

펑터에 항등 함수를 적용 했을 때 펑터 내부 데이터의 값이 변경 되지 않는다. 항등 법칙이 적용된다.

합성 법칙

이전 게시글에서 순수 함수들은 함수 합성이 가능하다고 이야기 하였다. 백문이 불여일견이라고 예시를 들어보자

const f = (value: number) => value + 1;
const g = (value: number) => value * 2;
 
// fmap(f.g)
const composeFunctor = functor.map((value) => f(g(value)));
// fmap(g).fmap(f)
const pipeFunctor = functor.map(g).map(f);
console.log(composeFunctor.valueOf === pipeFunctor.valueOf); // true

즉 펑터는 어떤 함수건, 순수 함수를 적용 할 때, 다른 사이드 이펙트 없이 작동되어야 한다는 것을 의미한다.

펑터 정리

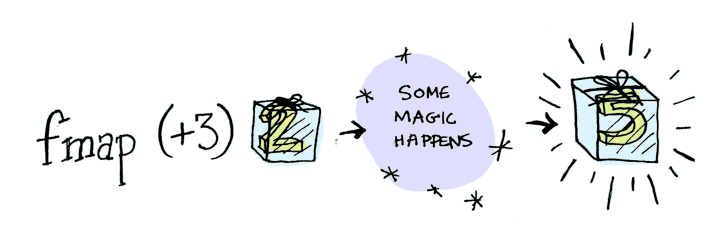펑터란 다양한 컨텍스트를 가진 데이터를 담고 새롭게 생성한 펑터를 반환하는 메소드를 가진 자료구조

결국 펑터란 어떤 데이터를 담은 자료구조로 그 데이터가 다른 데이터 타입으로 반환 가능하게 하는 자료구조이다.

펑터가 도대체 왜 필요할까?

다른 펑터들의 예시를 보지 않는다면, 펑터가 배열과 뭐가 다른데? 라고 생각이 들 수 있다.

펑터는 다양한 컨텍스트를 가진 데이터를 담고, 컨텍스트 별 행위를 처리하기 위해 사용된다.

배열은 List Functor 라고 정의되며 Array<T> 는 T 라는 하나의 컨텍스트(타입)를 가진 데이터들을 순차적으로 담고 있는 자료구조이다.

즉 배열은 펑터의 하위 개념일뿐 모든 펑터가 배열인 것이 아니다.

추후 기술할 펑터들을 이야기 하면 Maybe<T> 펑터는 데이터가 T 타입이 있을 수도 (Just<T>) 없을 수도 (Nothing) 를 의미하는 펑터도 존재한다.

Maybe<T> 가 확장된 형태인 Either<A,B> 펑터는 조건에 따라 Left<A> 데이터를 반환 할 수도 Right<B> 를 반환 할 수도 있다.

무지 종류가 많다. IO 펑터도 있고, Promise 펑터도 있고 뭐 .. 등등

이처럼 펑터는 다양한 컨텍스트를 펑터라는 자료구조로 추상화하고 map 메소드를 통해 함수 적용을 일반화 가능하게 하기 위해 필요하다.

Either 라는 펑터를 통해 조건부적인 컨텍스트를 컨트롤 하기도 하고, Maybe 펑터를 통해 연산의 결과과 있을 수도 있고, 없을 수도 있는 경우 타입 안정성을 취할 수 있다.

Maybe 펑터를 활용하는 방식

한 번 Maybe 펑터를 통해 타입 안정성을 처리하는 살펴보자

class Just<A> {
  constructor(public value: A) {}
 
  map<B>(f: (value: A) => B): Maybe<B> {
    return Maybe.of(f(this.value));
  }
 
  getOrElse(): A {
    return this.value;
  }
}
 
class Nothing {
  map<B>(f: (value: any) => B): Nothing {
    return this;
  }
 
  getOrElse<A>(defaultValue: A): A {
    return defaultValue;
  }
}
 
type Maybe<A> = Just<A> | Nothing;
 
namespace Maybe {
  export function of<A>(value: A | undefined | null): Maybe<A> {
    if (value === undefined || value === null) {
      return new Nothing();
    }
    return new Just(value);
  }
}

• 각 생성자들을 클래스로 표현한 이유는 타입 역할과 함께 생성자 역할을 함께 하기 위함이다.
• Maybe 가 클래스가 아닌 namespace 로 정의된 이유는 Maybe 자체는 타입을 의미하며 인스턴스를 생성하지 않기 때문이다. Maybe<A> 는 단순히 Just<A> | Nothing 을 의미한다.

준비는 끝났으니 이제 Maybe 타입을 이용해보자

이후 이런 시나리오를 생각해보자 , User 타입의 데이터에서 조건부로 존재하는 address 들을 가져와 로깅하고 싶다고 말이다. 이 때 User 가 없거나 address 가 없다면 Unknown 이란 단어를 로깅하도록 하자

interface User {
  name: string;
  address?: {
    street: string;
    city: string;
  };
}
 
const getUser = (id: number): User | null => {
  // ... (사용자 정보 가져오는 로직)
  if (id === 1) {
    return {
      name: "John Doe",
      address: { street: "123 Main St", city: "Anytown" },
    };
  } else if (id === 2) {
    return { name: "Jane Smith" };
  } else {
    return null;
  }
};

실생활의 데이터가 그렇듯 모든 어떤 값을 반환하는 함수가 항상 같은 타입의 값만을 반환하지 않는다. 그 데이터가 존재하지 않을 수도 있고, 에러가 발생할 수도 있기 때문이다.

Maybe 펑터와 Just , Nothing 에 존재하는 getOrElse 메소드를 활용하여 위에서 언급한 요구사항인

User 가 없거나 address.city 가 없다면 Unknow City 를 로깅하도록 메소드를 다음과 같이 짤 수 있다.

// 사용자 도시 정보 안전하게 가져오는 함수
const getUserCity = (id: number): Maybe<string> =>
  Maybe.of(getUser(id))
    .map((user) => user.address)
    .map((address) => address?.city);
 
const loggingUserCity = (id: number) => {
  const city = getUserCity(id).getOrElse("Unknown City");
  console.log(`User's city: ${city}`);
};
 
[1, 2, 3].forEach((id) => {
  loggingUserCity(id);
});
 
// User's city: Anytown
// User's city: Unknown City
// User's city: Unknown City

Just , Nothing 펑터를 반환하는 컨텍스트를 가진 Maybe 펑터를 이용해 if 문으로 처리 해야 했을 요구 사항을

함수들로만 이뤄진 표현식으로 표현하는게 가능해졌다.

이처럼 Functor 를 활용함으로서 다양한 컨텍스트를 가진 Functor 들의 조합으로 함수들의 조합으로 프로그래밍을 하는것이 가능해졌다.

짝짝짝

다양한 형태의 Functor 들은 나중에 개발 블로그를 함수형 프로그래밍 패턴으로 리팩토링 하면서 더 찾아봐야겠다. 지금은 이론만 먼저 공부해보자

적용형 펑터 (Applicative Functor)

컨텍스트에 데이터를 담아, 새로운 펑터를 반환하는 펑터는 충분히 효율적이지만 이런 문제가있다.

하나의 펑터를 이용해 다른 펑터를 만드는 것은 가능했지만 서로 다른 펑터를 조합하여 다른 펑터를 생성하는 것이 불가능하다.

현재 구현한 Just 를 이용해 Just<1> + Just<2> 를 구현하려면 이처럼 해야 한다.

class Just<A> {
  constructor(public value: A) {}
 
  map<B>(f: (value: A) => B): Maybe<B> {
    return Maybe.of(f(this.value));
  }
 
  getOrElse(): A {
    return this.value;
  }
 
  get valueOf(): A {
    return this.value;
  }
 
  static of<A>(value: A): Just<A> {
    return new Just(value);
  }}

매번 new Just(1) 형태로 생성하는 것이 귀찮으니 static 메소드를 만들어 Just.of(1) 처럼 사용 할 수 있게 만들어주고

펑터 내부 데이터에 직접 접근 할 수 있게 하도록 valueOf 라는 메소드도 함께 만들어주자

const just1 = Just.of(1);
const just2 = Just.of(2);
const just3 = Just.of(just1.valueOf + just2.valueOf);

구현하고자 한다면 이런 식으로 구현 하는 것이 가능하긴 하지만 찜찜한 부분이 존재한다.

펑터는 특정 컨텍스트 내부로 데이터를 담아 추상화 시키는 목적을 가지는데 , 추상화 시킨 데이터를 직접 꺼내는 valueOf 메소드는 펑터의 목적에 어긋난다.

또한 값이 무조건 존재한다는 Just 펑터라 그러려니 할 수 있지만 만약 Maybe.of(1) + Maybe.of(2) 였다면 하나라도 값이 Nothing 일 수 있기에 valueOf 로 접근하는 것은 오류를 발생 시킬 수 있다.

우리가 원하는 것은 펑터 내부에 존재하는 어떤 값들을 연산하여 새로운 펑터를 생성하는 것이다.

이러한 역할을 해주는 펑터를 적용형 펑터 라고 한다.

나무위키에서 정의한 적용형 펑터란 다음과 같다.

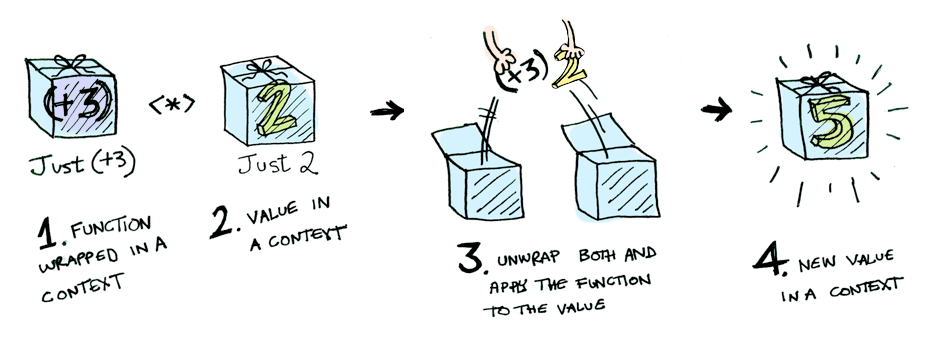적용형 펑터의 예시

함자 f에 대해 적절한 함수 pure와 <*>(apply)가 존재하여 다음 성질들을 만족할 때, f를 적용성 함자라고 하며, 임의의 타입 a에 대해 f a를 액션(action)이라 한다.

우선 정의를 한 번 더 되짚어야 하는데 어떤 함수를 펑터로 변경하는 행위를 리프팅(liffting) 이라 한다.

그 후 리프팅이 일어나 생성된 펑터를 안에 존재하는 함수를 action 이라 한다.

여기서 나는 모든 callable 한 값만 액션이라 하는줄 알았는데 펑터 안에 담긴 모든 값을 action 이라 지칭한다. 즉 적용형 펑터 안에 존재하는 함수도 액션, 일반 펑터 안에 담긴 값도 액션이라 한다.

class Just<A> {
  ...
  static pure<A>(value: A): Just<A> {
    return new Just(value);
  }
 
  /**
   * apply 가 실행되는 시점은 Just.value 가 callable한 action 형태일 때
   */
  apply<B extends A extends (args: T) => infer R ? R : never, T>(
    applicable: Maybe<T>
  ): Maybe<B> {
    if (this.value instanceof Function && applicable instanceof Just) {
      const func = this.value;
 
      return Maybe.of(func(applicable.value));
    }
    return new Nothing();
  }

다음과 같이 pure 메소드를 이용해 Just.pure(()=>{}) 를 이용하여 함수를 펑터 형태로 변경 하는 리프팅을 할 수 있도록 생성해주자

이후 apply 메소드를 이용하여 펑터간 연산을 지원 할 수 있도록 메소드를 생성해주자

여기서의 이 apply 메소드가 위 나무위키 예시에서 보았던 u <*> v 에 있는 <*> 를 의미한다.

예시를 통해 살펴보자

const just1 = Maybe.of(1);
const just2 = Maybe.of(2);
 
// 순수 함수 
const add = (value1: number) => (value2: number) => value1 + value2;
 
const liftedAdd = Just.pure(add); // 순수 함수를 리프팅 하여 적용형 함자로 생성
const result = liftedAdd.apply(just1).apply(just2);
console.log(result); // Just <{value : 3 }>
 
const wrongResult = liftedAdd.apply(just1).apply(Maybe.of(null));
console.log(wrongResult); // Nothing {}

적용형 함자를 통해 펑터 간의 연산을 처리하여 펑터 내부 데이터를 추상화 시킨 채로 순차적으로 연산을 가능하게 하였다.

적용형 펑터의 필수 조건

• 모든 함수 f :: a -> b와 액션 v :: f a에 대해 pure f <*> v ≡ fmap f v이다.
• 모든 액션 u :: f (a -> b)와 값 y :: a에 대해 u <*> pure y ≡ fmap (\f -> f y) u이다.
• 모든 액션 u :: f (b -> c), v :: f (a -> b)와 w :: f a에 대해 fmap (.) u <> v <> w ≡ u <> (v <> w)이다.

각 조건이 의미하는 것들을 하나씩 풀어가보자, 헷갈리지 않도록 다시 짚고 간다면 함수 f:: a ->b 의 f 는 함수의 이름, v:: f a 에서의 f 는 Functor<a> 를 의미한다.

1. 모든 함수 f :: a -> b와 액션 v :: f a에 대해 pure f <*> v ≡ fmap f v이다.

어떤 순수 함수 f 가 있고 Functor<V>가 있을 때 pure(f).apply(v) 의 값은 Functor<V>.map(f) 와 동치라는 것을 의미한다.

const increase = (value: number) => value + 1;
const liftedIncrease = Just.pure(increase);
const v = Maybe.of(1);
 
// prue f <*> v
const result1 = liftedIncrease.apply(v);
// fmap f v
const result2 = v.map(increase);
console.log(result1.getOrElse(0) === result2.getOrElse(0)); // true

2. 모든 액션 u :: f (a -> b)와 값 y :: a에 대해 u <*> pure y ≡ fmap (\f -> f y) u이다.

const y = 1;
const result3 = liftedIncrease.apply(Just.pure(y)); // u <*> pure y
const result4 = liftedIncrease.map((f) => f(y)); // u.map(f => f(y))
console.log(result3.getOrElse(0) === result4.getOrElse(0)); // true

3. 모든 액션 u :: f (b -> c), v :: f (a -> b)와 w :: f a에 대해 fmap (.) u <> v <> w ≡ u <> (v <> w)이다.

(.) 는 함수 합성을 의미한다.

보기엔 무슨 꼬부랑 꼬부랑 기호들로 이뤄진 거 같지만 그냥 각 액션들이 모두 순수하다면, 결합 법칙이 성립한다는 것을 의미한다.

순수 함수간의 결합 법칙이 성립함은 이전에 설명했기에 따로 예시는 들지 않는다.

회고

으갹 다행히 잼미니를 무진장 괴롭혀 조금은 이해가 간다. 이제 다양한 펑터들이 뭐가 있는지를 좀 알아놔야 하긴하는데

그래도 Maybe , Just , Nothing 펑터를 통해 원하는 값외에 다른 타입들을 가질 수 있는 다양한 컨텍스트를 펑터라는 타입 클래스 안에 가두고

그 펑터를 다룸으로서 if 와 같은 조건문의 사용을 지양하고, Functor 를 이용하여 타입 클래스 간의 함수 조합으로 프로그래밍이 가능하게 된다는 사실을 알게 되었다.

출처

1. Functors, Applicatives, And Monads In Pictures - adit.io
2. Types and Typeclasses - Learn You a Haskell for Great Good!
3. JS개발자는 아직도 모나드를 모르겠어요 | overthcode.io
4. 귀차니스트를 위한 펑터 | overcurried
5. FP in JS (자바스크립트로 접해보는 함수형 프로그래밍) - 함수자(Functor), Maybe
6. Haskell/특징/모나드 - 나무위키